Page 156 - INTRODUCCIÓN AL ANÁLISIS DE ALGORITMOS

INTRODUCCIÓN AL ANÁLISIS DE ALGORITMOS

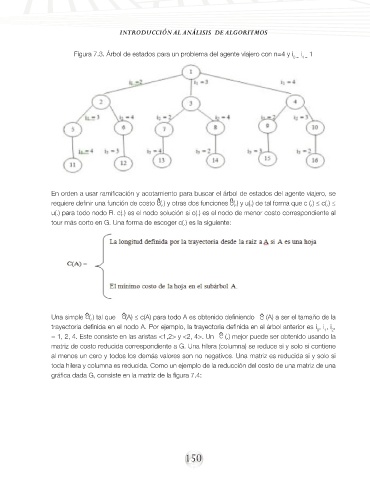
Figura 7.3. Árbol de estados para un problema del agente viajero con n=4 y i i 1
0 = 4 =

En orden a usar ramificación y acotamiento para buscar el árbol de estados del agente viajero, se
requiere definir una función de costo c(.) y otras dos funciones c(.) y u(.) de tal forma que c (.) ≤ c(.) ≤
u(.) para todo nodo R. c(.) es el nodo solución si c(.) es el nodo de menor costo correspondiente al
tour más corto en G. Una forma de escoger c(.) es la siguiente:

c
c
Una simple (.) tal que (A) ≤ c(A) para todo A es obtenido definiendo (A) a ser el tamaño de la
c
trayectoria definida en el nodo A. Por ejemplo, la trayectoria definida en el árbol anterior es i , i , i ,
1
0
2
c
= 1, 2, 4. Este consiste en las aristas <1,2> y <2, 4>. Un (.) mejor puede ser obtenido usando la
matriz de costo reducida correspondiente a G. Una hilera (columna) se reduce si y solo si contiene
al menos un cero y todos los demás valores son no negativos. Una matriz es reducida si y solo si
toda hilera y columna es reducida. Como un ejemplo de la reducción del costo de una matriz de una
gráfica dada G, consiste en la matriz de la figura 7.4:

150