Page 21 - INTRODUCCIÓN AL ANÁLISIS DE ALGORITMOS

INTRODUCCIÓN AL ANÁLISIS DE ALGORITMOS

cota SuperIor aSINtótIca

La notación O (gran O), O (g(n)) es el conjunto de todas las funciones f para las cuales existen cons-
i
tantes enteras positivas c y n tales que para n >= n se cumple lo siguiente:
o 0
f(n) < cg(n)
i
cg(n) es una “cota superior” de toda f para n > n .
i 0
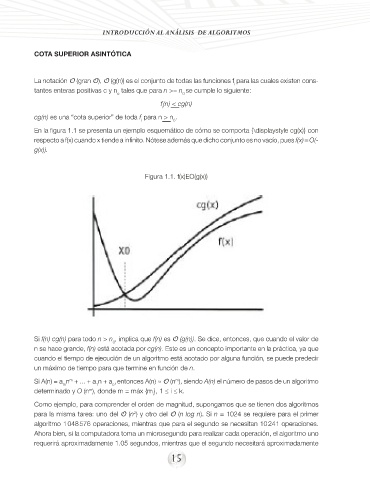
En la figura 1.1 se presenta un ejemplo esquemático de cómo se comporta {\displaystyle cg(x)} con
respecto a f(x) cuando x tiende a infinito. Nótese además que dicho conjunto es no vacío, pues f(x) = O(-
g(x)).

Figura 1.1. f(x)EO(g(x))

Si f(n) cg(n) para todo n > n , implica que f(n) es O (g(n)). Se dice, entonces, que cuando el valor de
0
n se hace grande, f(n) está acotada por cg(n). Este es un concepto importante en la práctica, ya que
cuando el tiempo de ejecución de un algoritmo está acotado por alguna función, se puede predecir
un máximo de tiempo para que termine en función de n.

Si A(n) = a n + ... + a n + a ,entonces A(n) ≈ O (n ), siendo A(n) el número de pasos de un algoritmo
m
m
m 1 o
determinado y O (n ), donde m = máx {m}, 1 ≤ i ≤ k.
m
i
Como ejemplo, para comprender el orden de magnitud, supongamos que se tienen dos algoritmos
para la misma tarea: uno del O (n ) y otro del O (n log n). Si n = 1024 se requiere para el primer
2
algoritmo 1 048 576 operaciones, mientras que para el segundo se necesitan 10 241 operaciones.
Ahora bien, si la computadora toma un microsegundo para realizar cada operación, el algoritmo uno
requerirá aproximadamente 1.05 segundos, mientras que el segundo necesitará aproximadamente

15