Page 83 - INTRODUCCIÓN AL ANÁLISIS DE ALGORITMOS

INTRODUCCIÓN AL ANÁLISIS DE ALGORITMOS

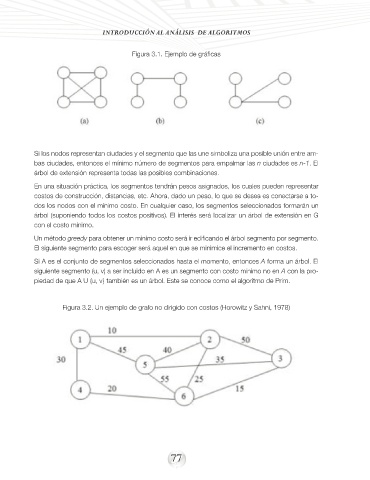
Figura 3.1. Ejemplo de gráficas

Si los nodos representan ciudades y el segmento que las une simboliza una posible unión entre am-
bas ciudades, entonces el mínimo número de segmentos para empalmar las n ciudades es n-1. El
árbol de extensión representa todas las posibles combinaciones.

En una situación práctica, los segmentos tendrán pesos asignados, los cuales pueden representar
costos de construcción, distancias, etc. Ahora, dado un peso, lo que se desea es conectarse a to-
dos los nodos con el mínimo costo. En cualquier caso, los segmentos seleccionados formarán un
árbol (suponiendo todos los costos positivos). El interés será localizar un árbol de extensión en G
con el costo mínimo.
Un método greedy para obtener un mínimo costo será ir edificando el árbol segmento por segmento.
El siguiente segmento para escoger será aquel en que se minimice el incremento en costos.

Si A es el conjunto de segmentos seleccionados hasta el momento, entonces A forma un árbol. El
siguiente segmento (u, v) a ser incluido en A es un segmento con costo mínimo no en A con la pro-
piedad de que A U {u, v} también es un árbol. Este se conoce como el algoritmo de Prim.

Figura 3.2. Un ejemplo de grafo no dirigido con costos (Horowitz y Sahni, 1978)

77